1980年，心理学家William James出版了第一部论述人脑结构及功能的专著《心理学原理》，首次提出:
“一个神经细胞受到刺激激活后可以把刺激传播到另一个神经细胞，并且神经细胞激活是所有细胞输入叠加的结果！”
为人们认识神经网络的活动打开了理论的天窗。基于这个理论假设，从1943年开始，神经网络经历的曲折荡漾的发展，经历了数次的大起大落；理论模型也从单一的神经元感知机开始，发展到包含一个隐藏的多层感知机网络，到现在已卷积神经网络为代表的深度卷积神经网络。
本文以神经网络的发展为线索，从卷积神经网络的结构和应用两个方面进行简单阐述。
1. 什么是卷积神经网络
认识卷积神经网络之前首先要了解两个基本的概念: 1、什么是卷积；2、什么是神经网络。
1.1 什么是卷积
- 从图像的角度来看卷积: 就是卷积模板在图像上滑动，把对应位置上的元素相城相加得到最终结果的过程。如果考虑翻转则就需要翻转卷积模板。
卷积核的大小是奇数，如3x3,5x5,7x7等；在cnn的世界里，卷积就是通过不同的卷积核，在不同的图像尺度下，滑动来计算卷积特征的。通过修改卷积核的参数，可以实现对图像进行锐化、模糊等操作，从而检测出图像中的视觉特征；训练cnn的过程，其实也是学习这些卷积和参数的过程。在有限的范围内，使用的卷积核越多，可以学习到的图像特征也就越多。
1.2 什么是神经网络
按照William James的观点，人工神经网络是基于神经元假设的一种数学描述，是从信息处理的角度将人脑神经元网络进行抽象，从而建立某种模型，可以让神经元按照不同的连接方式组成不同网络的一种数学方法。神经元由大量的节点连接，这个节点称之为激活函数。常见的激活函有: sigmoid、tanh和Relu;
$$
\begin{eqnarray}
Sigmoid(x) = 1/(1+e^{-x}) \\
tanh(x)=\frac{1-e^{-2x}} {1+e^{-2x}} \\
relu(x)=max(0,x)
\end{eqnarray}
$$
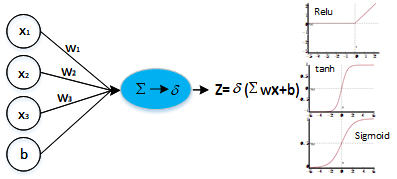三种常用的激活函数
而神经元数学模型就是输入向量X经过加权，通过激活函数f过滤，输出y，也就是：
$$
\begin{equation}
y=f(w_1*x_1+w_2*x_2+b)
\end{equation}
$$
这就是感知机的数学表达。$f(x)$但是它只能解决线性问题，对于非线性问题，感知机就无从下手了，比如：异或问题。为了解决非线性问题，又在感知机的基础上提出了前馈神经网络多层感知机 ；如图，给定一组特性向量:
$$x=(x_1, x_2, x_3, ….)$$ 通过输入层输入到MLP网络，网络中的隐藏层，相对于增加感知机的决策平面，从而引入多个决策节点，通过级联这些神经元，就可以将原本单个感知机的线性表示表示成多个分段的线性表示，这样就将线性的问题转换成了非线性。也就是无线逼近的积分结果，这样就可以将学习特征用级联的线性表达学习复杂的非线性模式。
1.3 什么是卷积神经网络
卷积区别于传统的前馈神经网络的重要是，多层感知机表达的前馈神经网络的每个神经元都和前一层的输入全部相连接，是一种完全连接的模式；而卷积神经网络通过卷积核与前一层的输入相连接，卷积核的尺寸(感受野)就是卷积神经网络的连接范围，是一种局部的连接的方式。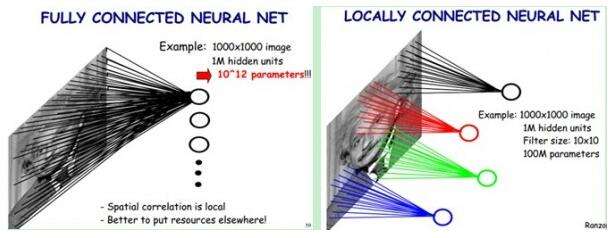
上图中，假设输入图像是一个1000*1000的图像，左边全连接的网络有100w个隐层的神经元，每个神经元都与输入图像的每个像素相连，那么这个网络就有1000*1000*100w = 10^12个连接；右边局部连接的网络每个节点与输入图像有10*10（实际连接的卷积和尺寸是奇数）的连接，那么100w个隐层的神经元的连接个数是10*10*100w = 10^8，比全连接少了4个数量级。除此之外卷积神经网络还有另外一个特新就是权值共享。也就是在同一层的卷积核对应的参数是相同卷积核。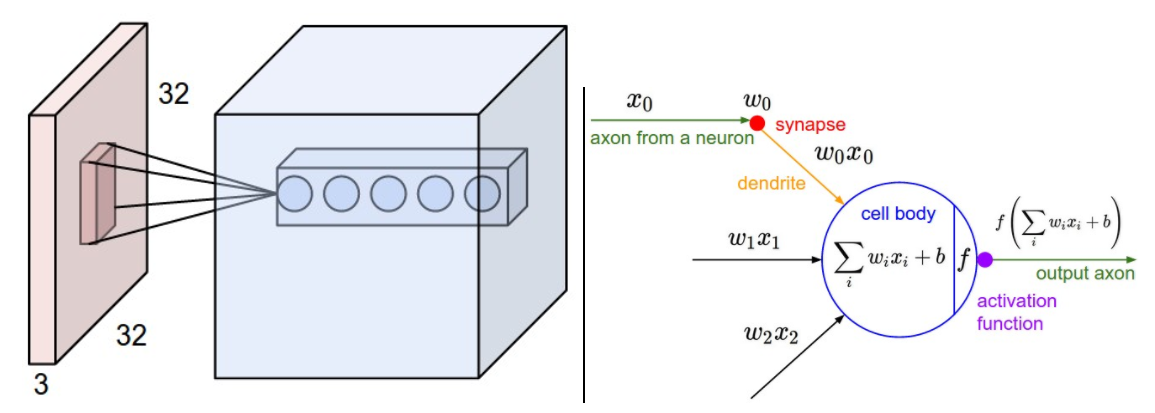
上图是一个卷积的示例，左边红色为32*32*3的输入数据，蓝色部分是一层卷积网络；右边为卷积网络的神经元数学表述，是和普通的前馈神经网络相同的模型；除了卷积和全连接的区别，卷积神经网络结构也差别很大，是由卷积核的宽度、高度和卷积层数表述的一种长、宽、深度的三维模型，这里的深度就是卷积神经网络的网络层数；
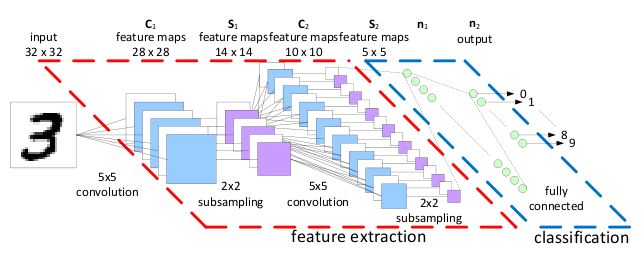
1.3 卷积神经网络的基本结构
经典的卷积神经网络是包含：输入层、卷积层、池化层、激活层、全连接层以及输出层构成的。如下图，为LeNet-5的CNN模型:
